微积分与优化 Calculus & Optimization

深入理解偏导数、梯度、链式法则与拉格朗日乘数法在优化问题中的应用

3
算法类型
5
核心概念
∞
应用场景
∇

偏导数与梯度

Partial Derivatives & Gradient

核心概念

偏导数描述函数在某个方向上的变化率，梯度是所有偏导数组成的向量，指向函数值增长最快的方向。

梯度定义
∇f(x,y) = (∂f/∂x, ∂f/∂y)
gradient points to steepest ascent
∂f/∂x
X方向偏导数
∂f/∂y
Y方向偏导数
⇒

链式法则

Chain Rule

复合函数求导
∂z/∂x = (∂z/∂u)(∂u/∂x) + (∂z/∂v)(∂v/∂x)

当z = f(u,v), u = g(x,y), v = h(x,y)时，链式法则帮助我们计算复合函数的偏导数。

λ

拉格朗日乘数法

Lagrange Multipliers

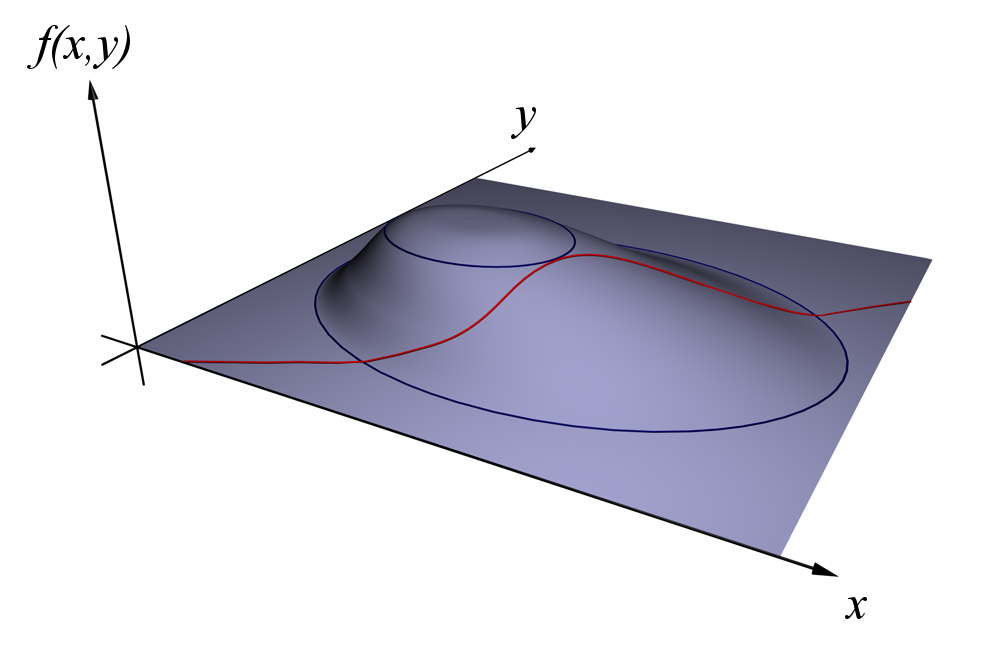
拉格朗日乘数法可视化
约束优化公式
∇f(x,y) = λ∇g(x,y)
g(x,y) = c
1
建立拉格朗日函数 L(x,y,λ) = f(x,y) - λ(g(x,y) - c)
2
求解梯度方程组 ∇L = 0
3
验证解的性质（最大值/最小值）
↓

梯度下降算法

Gradient Descent

BGD
批量梯度下降
稳定但慢
SGD
随机梯度下降
快速但噪声
MBGD
小批量梯度下降
平衡选择

算法收敛路径

Convergence Visualization

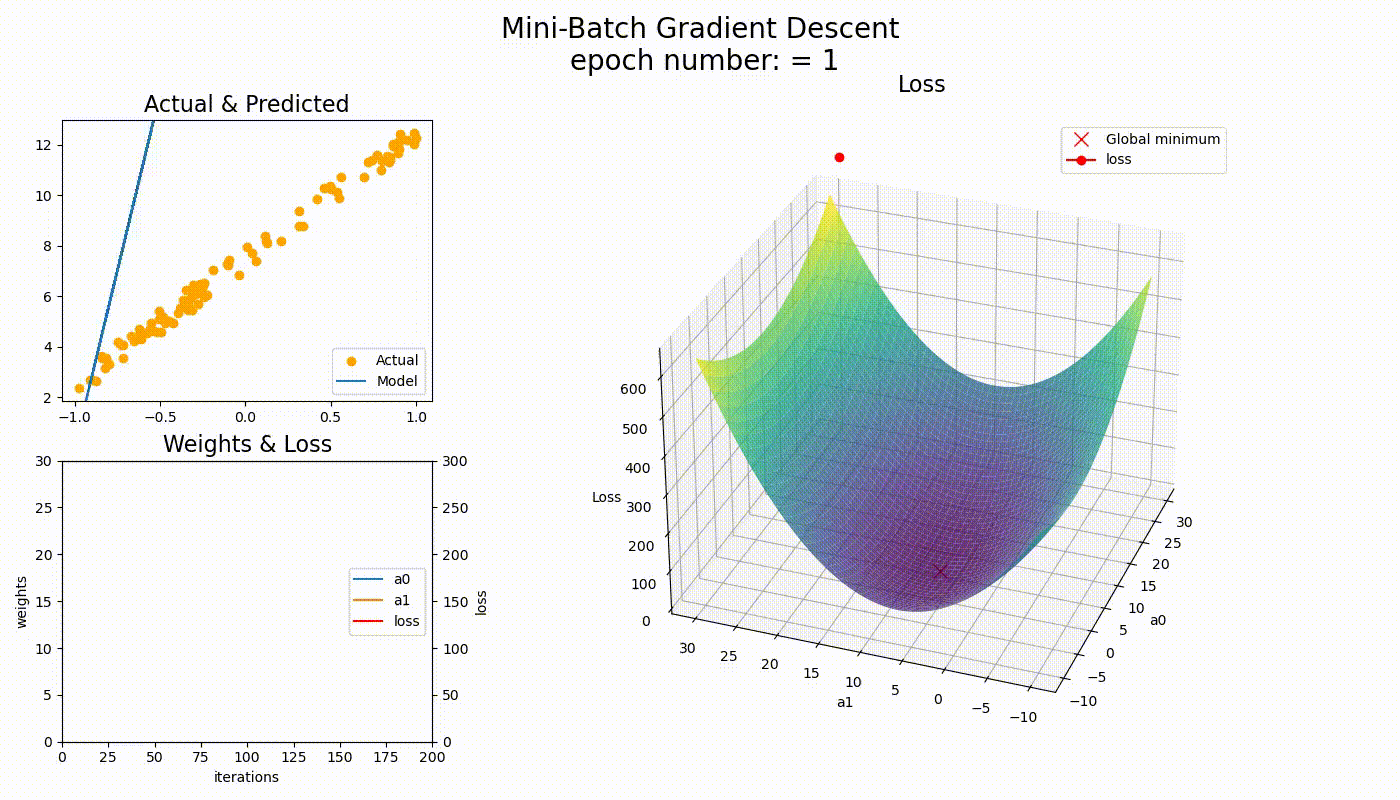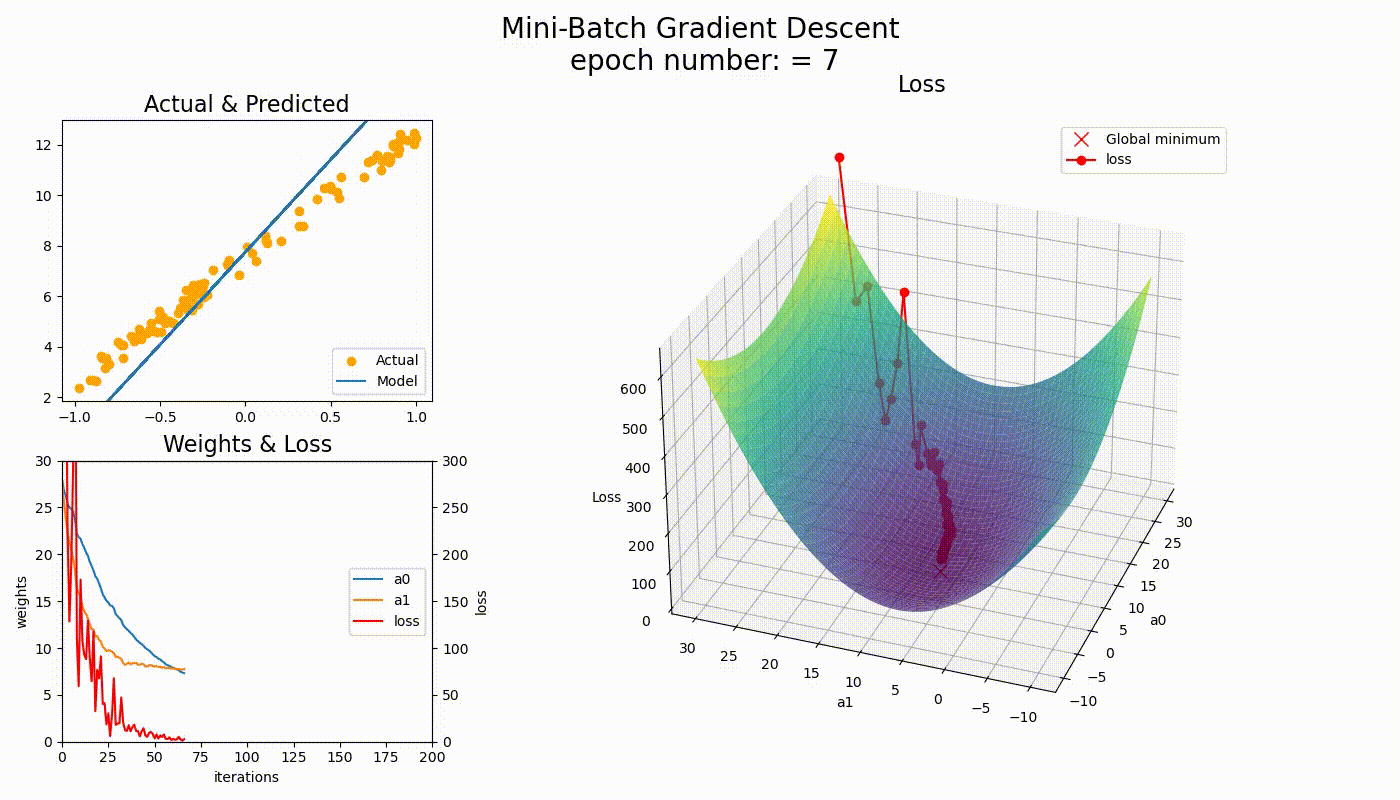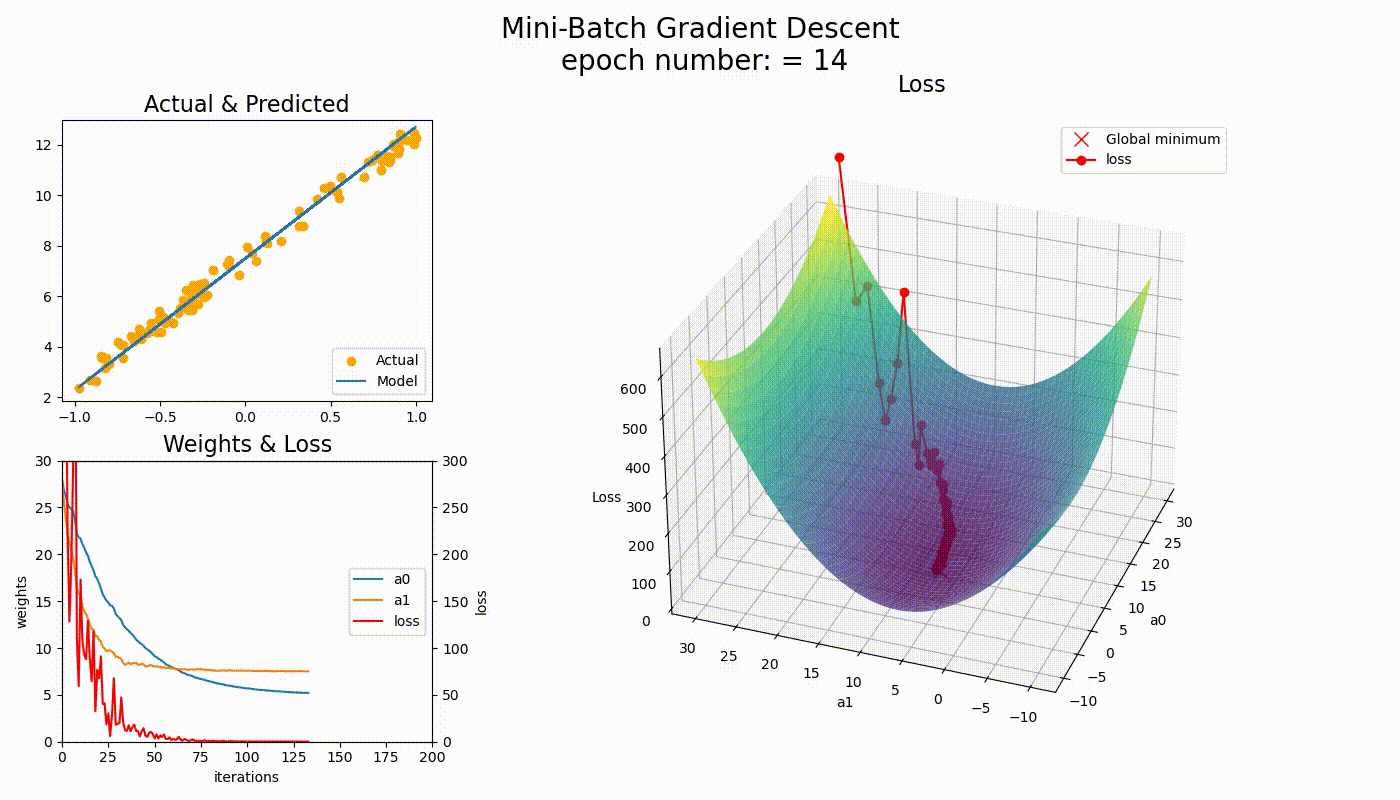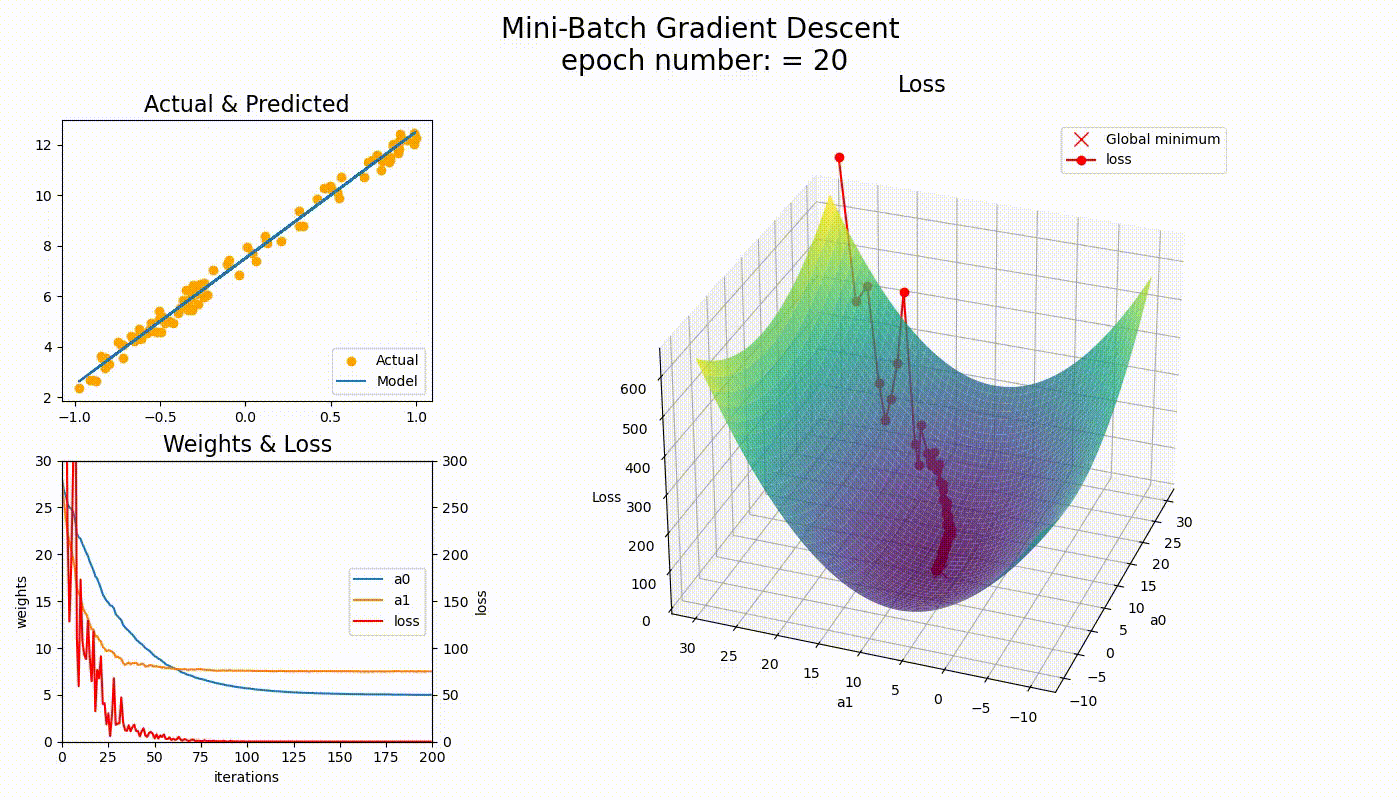
梯度下降算法对比动画

关键观察

  • • BGD路径平滑，直接朝向最优解
  • • SGD路径波动，但能逃离局部最优
  • • MBGD介于两者之间，实用性最强
∞

大规模模型优化

Large-Scale Optimization

Adam优化器
自适应学习率，适合大部分场景
ZeRO优化
内存优化，支持万亿参数模型
混合精度训练
FP16/FP32结合，加速收敛
2

二阶优化

Second-Order Methods

牛顿法
x_{k+1} = x_k - H^{-1}∇f(x_k)
O(n²)
计算复杂度
快速
收敛速度

使用海森矩阵信息，收敛更快但计算成本高

🎯

应用场景

Real Applications

机器学习
神经网络权重优化
深度学习
大模型参数调优
工程优化
约束条件下的最优设计

核心要点总结

Key Takeaways

理论基础

  • • 偏导数是梯度的基础
  • • 链式法则处理复合函数
  • • 拉格朗日法解约束优化

算法实践

  • • BGD稳定，SGD快速
  • • MBGD是实践首选
  • • Adam适合大规模训练

视频资源

Video Learning

梯度下降视频
Gradient Descent in 3 minutes
Visually Explained

推荐观看Khan Academy和3Blue1Brown的微积分系列视频，直观理解概念。